
Todas las expresiones algebraicas, generalmente se escriben de varias maneras. Algunas de ellas son comunes y otras son notables. Ante esta situación es necesario una clasificación de todas estas expresiones.
Índice
Definición de polinomios especiales
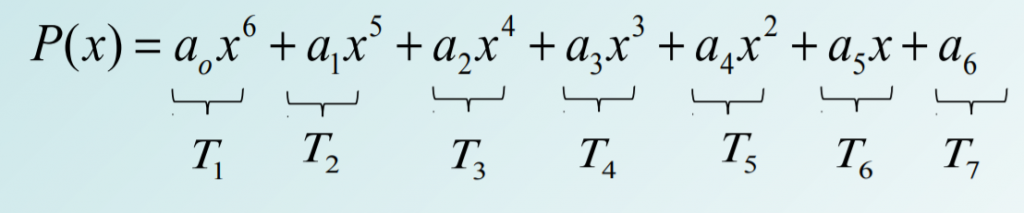
Son todas las expresiones algebraicas enteras, en las cuales sus elementos, como las variables y sus grados, y la forma cómo se escriben, tienen algunas propiedades implícitas que las hacen notables ante otros polinomios. Estas pueden ser: ordenados, completos, homogéneos, idénticos, opuestos y nulos.
Polinomios ordenados
Los polinomios, se pueden ordenar de manera ascendente o descendente. Para definir este orden, se toma en consideración el grado de la variable. En el caso de que haya dos o mas variables, se ordena en función de una de las variables, para este procedimiento, se elige una de ellas, y se le da el orden correspondiente.
Ejemplo de polinomios ordenados con una sola variable
El orden que se le da a los siguientes polinomios, está en función de las variables “x” y “y” respectivamente. Cada variable de los polinomios, es denomina ORDENATRIZ
2x5 + 3x2 + x1 – 6 2 – m1 + 3m2 + 7m4
Orden ascendente Orden descendente
En los ejemplos, la variable “x” es ordenatriz ascendente. La variable “y” es ordenatriz descendente o decreciente
Ejemplos de polinomios ordenados con dos o más variables
Cuando hay dos variables,
2a3b + 3a2b3 + a1b2– 6 2y3 – y1z2 + 3y2z + 7y3
Orden ascendente Orden descendente
en función de “a” en función de “y”
Polinomios completos
Estos polinomios, pueden ser de una variable y/o de dos o más variables:
Polinomios completos en una sola variable
Un polinomio completo, es la expresión que tiene el número de términos, igual al grado de la expresión aumentado en uno. También, la diferencia de un grado con consecutivo, siempre es uno
2a3+ 3a2 + a1 – 6 1 – u1 + 3u2 – 2u3 + 7u4
También se puede escribir de la siguiente forma:
2a3+ 3a2 + a1 – 6 a0 1 a0 – u1 + 3u2 – 2u3 + 7u4
Orden ascendente Orden descendente
Polinomios completos con más de una variable
Para determinar un polinomio completo con más de una variable, primero se debe elegir una de ellas, y después dar el orden correspondiente.
2x3y + 3x2y3 + x1y2 – 1 2n3 – m1n2 + 3m2n + 7m3
Se puede escribir la expresión de la siguiente manera:
2x3y + 3x2y3 + x1y2 – 1x0 2n3m0 – m1n2 + 3m2n + 7m3
Ordenado en función a “x” Ordenado en función de m
Polinomios homogéneos
Un polinomio homogéneo, es aquel que está compuesto por más de una variable, y los términos tienen los mismos valores absolutos. En otras palabras, un polinomio, de más de una variable es homogéneo, si dichos términos poseen el mismo grado absoluto, llamado grado de homogeneidad. Ejemplo:
2x3y2 + 3x2y3 + x4y1
En este ejemplo, los grados absolutos de los tres términos, tienen la misma cantidad de cinco. Y reciben el nombre, de, polinomio homogéneo de grado 5
Polinomios idénticos
Son aquellas expresiones que tienen los mismos términos algebraicos. Entonces se cumple:
Si, P(x) = ax3 + bx2 + c es idéntico a Q(x) = 3x2 + 2x3 – 5, entonces a=3, b=2 y c=-5
Polinomios opuestos
Los polinomios opuestos, son las expresiones que tienen los mismos coeficientes, pero de signos contrarios. Ejemplos:
1) 2y2 – 5y3 + y4, su opuesto es, -2y2 + 5y3 – y4
2) -x3y2 + 3x2y3 + 5x4, su opuesto es, +x3y2 – 3x2y3 – 5x4
3) 2x3 + 3x2+ y – 2, su opuesto es, -2x3 – 3x2 – y + 2
Polinomios nulos
Polinomio nulo, es aquel que su valor numérico es cero. Cumple la condición: P(x) = ax2 + bx – c =, tal que a = b = c = 0
Ejemplos:
1) 0m2 – 0m + 0
2) 0y2 + 0y
3) 0x3 + 0x2 + 0x – 0